Experiments with CIFAR10 - Part 2

Background

This is a continuation of the previous post Experiments with CIFAR10 - Part 1. In that post, we looked at quickly setting up a baseline Resnet model with ~94% accuracy on CIFAR10. We also looked at alternatives to Batch Normalization and explored Group Normalization with Weight Standardization. Building up on it, in this post we’re going to look at different ways to tune the learning rate with schedulers along with more advanced methods to achieve better generalization like Stochastic Weight Averaging (SWA).

A couple of months ago, I came across this tweet chain and the corresponding paper surveying different optimizers and learning rate schedulers.

For most applied problems, the optimizer choice is largely irrelevant. Use good defaults like ADAM or SGD.

The most important thing is to tune the learning rate - most gains come from here.

If you have limited budget and don’t know what to tune, learning rate is it! https://t.co/QYFWLgsNhU

— Grid.ai (@gridai_) October 10, 2020

I’ll be using the different LR schedulers implemented in torch.optim.lr_scheduler but it is also very easy to implement a scheduler of your own in the framework of your choice.

LR Schedulers

Step Based LR schedulers

In the previous post, we used the Multi Step LR scheduler as the default scheduler. It is very similar to the Step LR scheduler, the only difference being that the former decays the learning rate at pre-defined milestones whereas the latter decays the learning rate at a single fixed interval. The rate of decay is controlled by the gamma parameter in PyTorch and is multiplicative. So, for example, if we define a Multi-Step LR scheduler as follows

torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[25,40], gamma=0.1)

The graph of our learning rate (starting from 0.05) over the training budget (50 epcohs in the last post) will look like

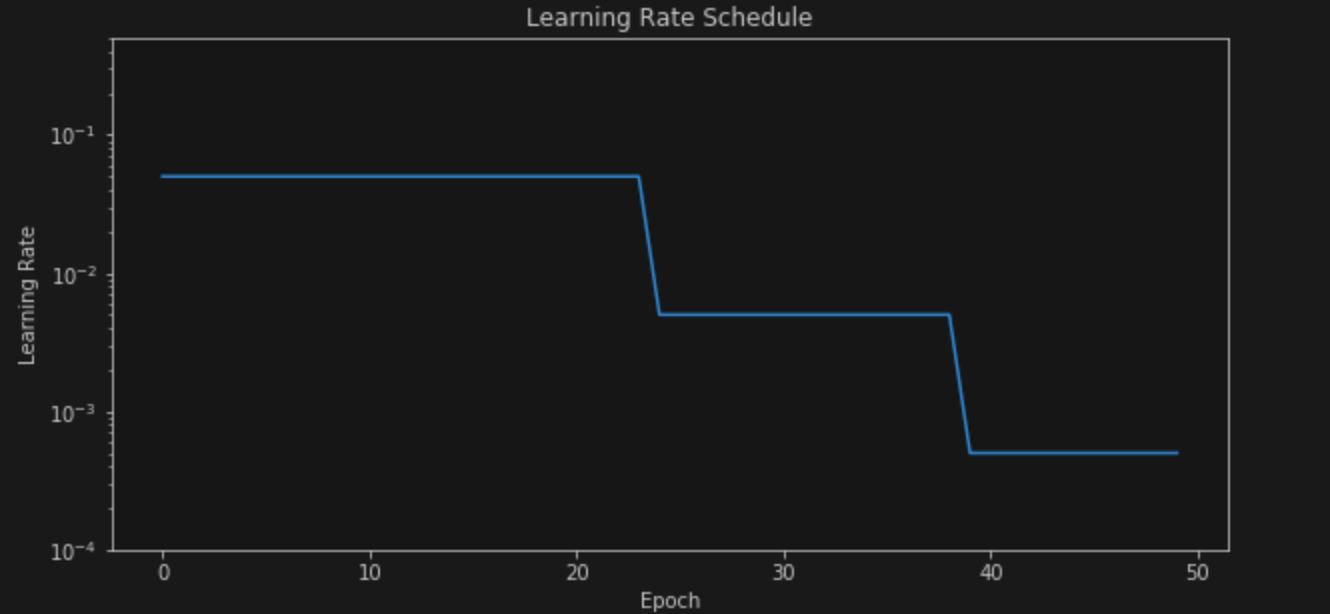
As seen in the last post, this LR scheduler reaches ~93.7-94% over 50 epochs.

Cosine Annealing based LR schedulers

LR schedulers that decay the learning rate every epoch using a Cosine schedule were introduced in SGDR: Stochastic Gradient Descent with Warm Restarts. Warm restarts are also used along with Cosine Annealing to boost performance. Warm restarts mean that the learning rate is pumped up to the max value again after certain epochs (I assume this helps in achieving better generalization and also escape local valleys.) In PyTorch, it can be implemented as follows

'''Cosine Annealing
    This will decay the learning rate
    from max value to eta_min using cosine annealing over T_max epochs'''
torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=epochs, eta_min=0)

'''Cosine Annealing with Warm Restarts
    This will decay the learning rate
    from max value to eta_min over T_0 epochs first,
    then restart and decay over T_0 * T_mult,
    then over T_0 * T_mult^2 and so on'''
torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0=epochs//3, T_mult=2, eta_min=0)

The corresponding graphs over the training budget look like

Cosine Annealing

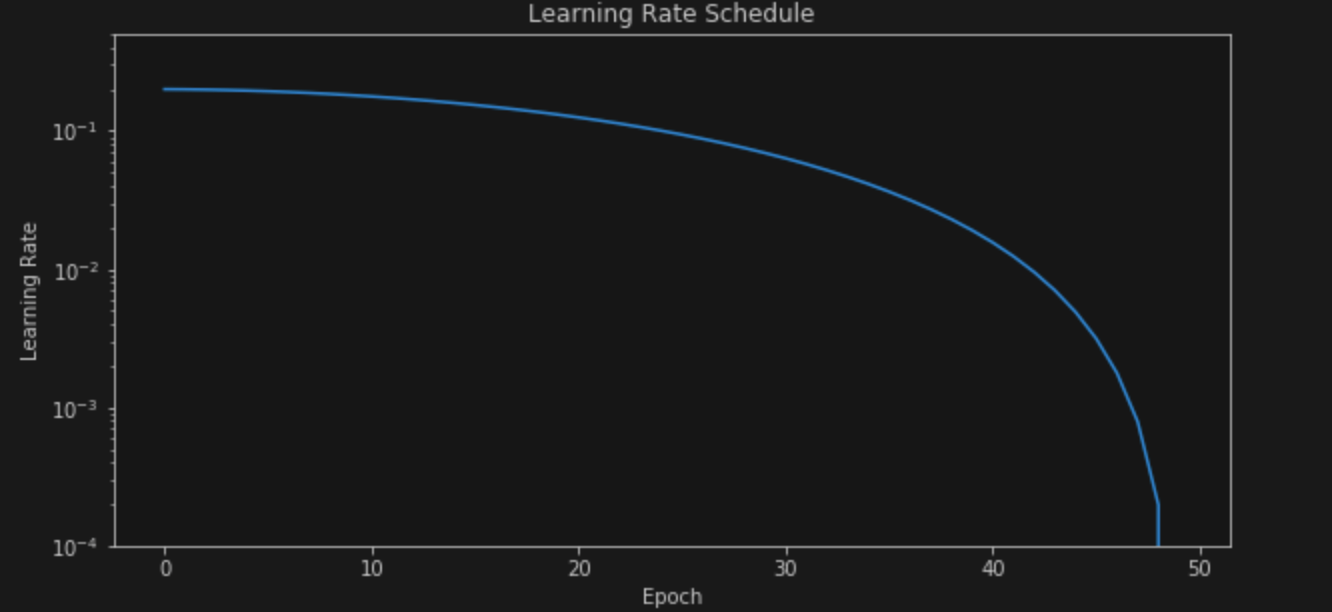
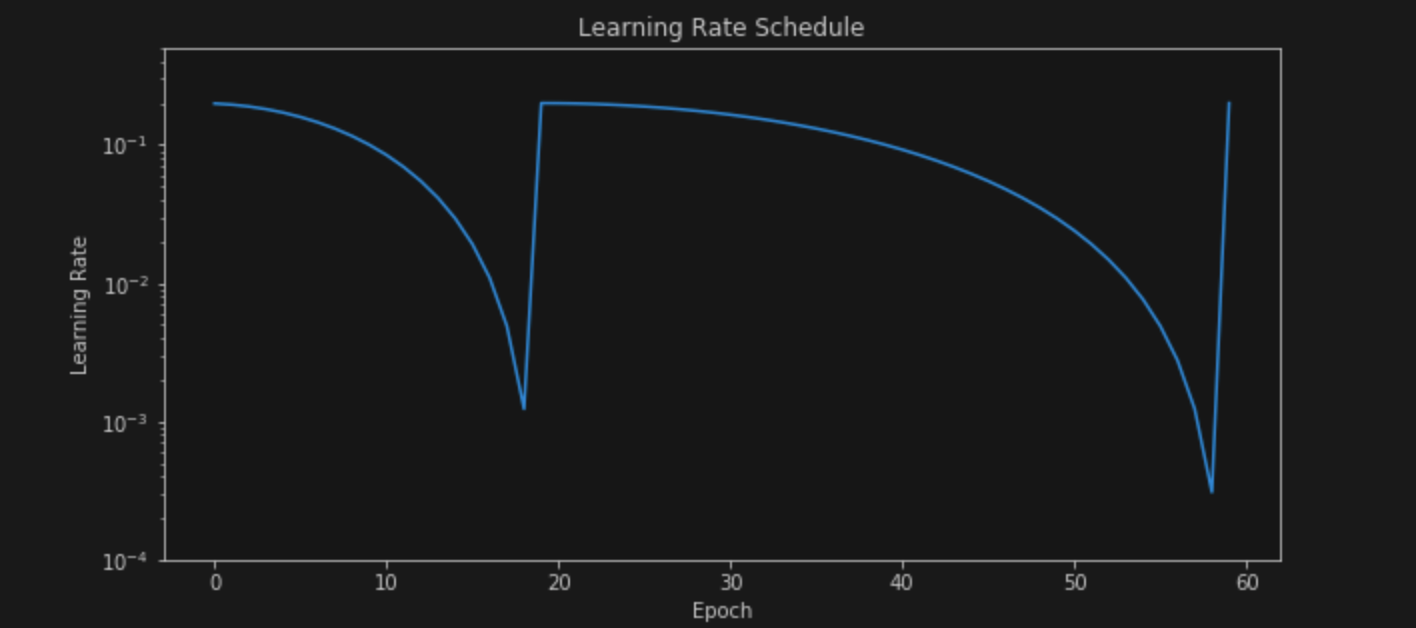
These schedulers also reache ~93.8-94% over 50 and 60 epochs respectively.

Cyclical LRs and One Cycle LR scheduler

As we saw above with Warm Restarts, LR schedulers can sometimes be cyclical. In Cosine Annealing with Warm Restarts, the cycle length multiples by T_Mult each cycle and follows a cosine schedule for decay. But there are also Cyclic LR schedulers that follow constant cycles and decay the learning rate with a constant frequency. These are implemented in torch.optim.lr_scheduler.CyclicLR and the paper Cyclical Learning Rates for Training Neural Networks describes them in more details. One can control how many cycles to use in the training budget.

With a slight modification, we come to the One Cycle LR scheduler. Accoring to the Pytorch documentation,

The 1cycle policy anneals the learning rate from an initial learning rate to some maximum learning rate and then from that maximum learning rate to some minimum learning rate much lower than the initial learning rate.

According to the paper Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates in which it was propesed, this can be used to accelerate training speeds. This is proven in my simple experiments (code at playing_with_lr_schedulers.ipynb). The same model achieves ~94.65% accuracy with this scheduler over 50 epochs and ~93.8% accuracy in just 30 epochs. This scheduler can be implemented as follows

torch.optim.lr_scheduler.OneCycleLR(
    optimizer,
    max_lr=0.1,
    total_steps=(epochs * math.ceil(50000/HPS['batch_size'])),
    pct_start=0.3,
    anneal_strategy='cos',
    cycle_momentum=True,
    base_momentum=0.85,
    max_momentum=0.95,
)

There are many options to customize the scheduler like cycling momentum, controlling the percent of training budget when the learning rate rises, the anneal strategy and so on. More details are in the documentation linked at the start. The graph of the learning rate for this scheduler looks like

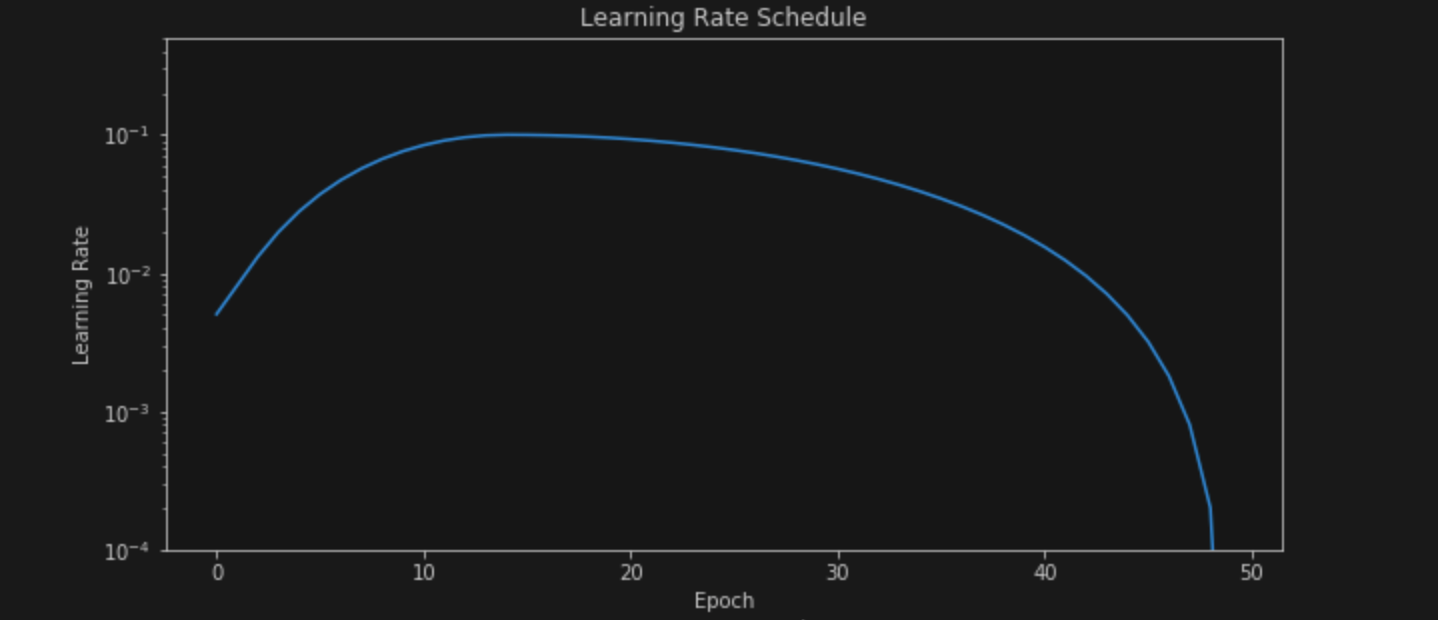
As you can see, it goes up to the maximum for around 30% of the training budget and then starts decaying.

Notes on LR schedulers

Apart from the ones discussed above, there are more advanced LR schedulers like ReduceLROnPlateau that dynamically change the learning rate when a corresponding metric stops improving. There’s also LambdaLR that calculates the multiplicative factor using a lambda function. It is also fairly easy to implement your own scheduler, and you might see many custom schedulers in PyTorch implementations of research papers.

One important caveat to look out for when integrating the LR scheduler in your training code is the interval at which it operates. Some schedulers step every batch, while some step every epoch. Getting the step interval wrong can lead to all sorts of problems.

From the documentation, Batch LR schedulers can be used like

for epoch in range(10):
    for batch in data_loader:
        train_batch(...)
        scheduler.step()

Whereas Epoch LR schedulers can be used like

for epoch in range(10):
    for batch in data_loader:
        train_batch(...)

    scheduler.step()

Carefully go through the documentation when using an LR scheduler.

Stochastic Weight Averaging

SWA was introduced Pavel Izmailov et al in the paper Averaging Weights Leads to Wider Optima and Better Generalization and is an excellent method to improve generalization. It was recently included in PyTorch 1.6 and this makes it extremely easy to implement. SWA can help achieve significant improvements in performance for an additional 25-50% of the training budget. To get an intuition of how SWA works, imagine there’s a valley with a lake in the Loss Landscape. SGD converges at the boundary of the lake, and SWA travels along the boundary and averages those positions to reach the center of the lake. The PyTorch blog post linked above includes the implementation details, so I will just show the graph of the learning rate and the loss and accuracy plots for the following experiment - OneCycleLR for the first 20 epochs and then SWA using SGD optimizer with a high learning rate of 0.01.

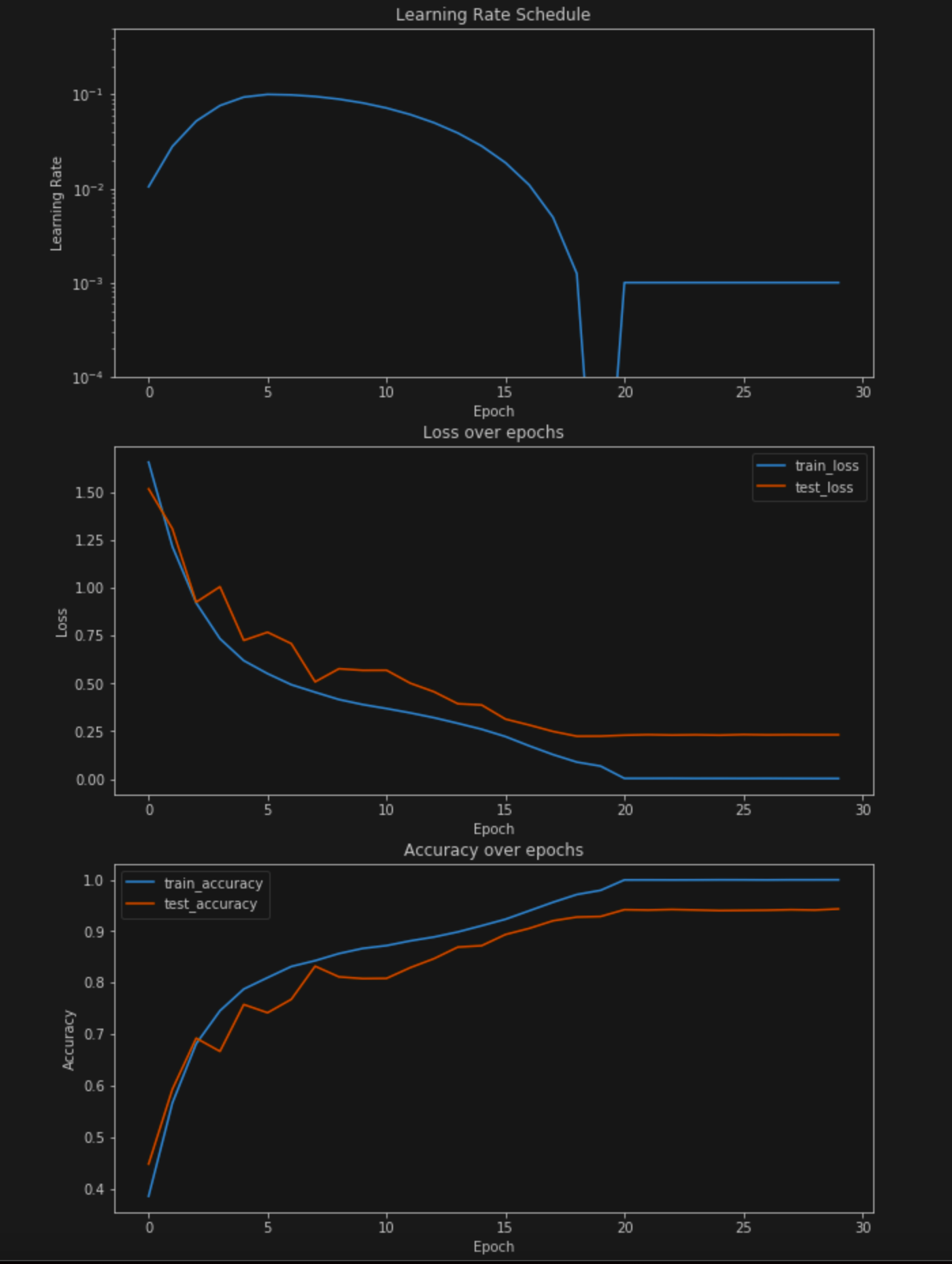
As you can see, the loss and accuracy might not show improvements during individual iterations of SWA, but the improvement becomes visible in the end when the weights of these iterations are averaged (in this case weights were recorded at the end of each epoch). This particular experiment achieves ~94% with just 30 epochs in total.

Conclusion

In this post, we looked at different LR schedulers and saw how they can be combined with methods like SWA to tune your deep learning models and achieve significant improvements in performance. There’s still lots of experiments that can be done with just CIFAR10 and Resnets like different regularization techniques including ShakeShake and ShakeDrop, transfer learning and finetuning using weights from different models trained on bigger datasets, Deep Ensembling and Multi-SWA(G), etc. I will try to explore some of it and write about it in the continuation of this series. Feel free to comment or reach out if I’m missing something important.